結城浩の「コミュニケーションの心がけ」2015年9月29日 Vol.183
はじめに
おはようございます。 いつも結城メルマガをご愛読ありがとうございます。
微妙に曇っている天気のときもありますが、 暑すぎず、寒すぎず、いい感じの気候です。
秋ですね。
* * *
ベクトル本の話。
今年の秋に刊行される予定の『数学ガールの秘密ノート/ベクトルの真実』。 現在は出版社から初校が届くのを待っているところ。 おそらく今週の終わりくらいには届くと思います。
それまでの時間、別の仕事に向かうこともできるのですが、 気になる点がいろいろあるので、もう一度全体を読み返しています。 また、レビューアさんから送られてくるレビューメールの反映も再チェック。 毎日ちまちまと文章を直したり、図版を改善したり。あれこれ大忙し。
今月どこかのタイミングで、 恒例の無料サイン本プレゼント企画を行いたいと思っていますが、 まだ日程は決まっていません。
毎回思うのですけれど「本を書く」というのは、 「教育・学習」に密接に関係があると思っています。 一つは著者から読者に向けて大切なことを伝えるという意味の教育・学習ですが、 もう一つは著者自身にとっての「教育・学習」です。
自分の知らないことを本に書くことは不可能ですから、 本を書くためには、少なくともその本に書けるほどの深さ・広さで、 ものごとを知っている必要があります。ですよね。 ですから書くことを通して著者は学ぶ。学ばされる。
今回もベクトル本を書きながら、結城はベクトルについて多くを学びました。 数学ガールたちの会話に耳をすませながら、 「なるほど!」と膝を打つことが何度もありました。 数学って、学ぶって、おもしろいですよね!
◆『数学ガールの秘密ノート/ベクトルの真実』
https://bit.ly/girlvector
* * *
そういえば、ジュンク堂池袋本店では「結城浩書店」 というミニコーナーが展開されています。 結城の本はもちろんのこと、結城がオススメする本がずらりと並んでいます。 私の紹介文もありますよ。
もし池袋にいく機会がありましたら、ぜひお立ち寄りくださいね!
少なくとも、2015年9月末までは「結城浩書店」オープンしているそうです。
* * *
忙中閑あり。
結城はiPhoneでパズルゲームをするのが大好きです。 最近は、"Lara Croft GO" というゲームを楽しんでいましたが、 先日全画面コンプリートできました。
◆"Lara Croft GO" Launch Trailer(紹介動画)
https://youtu.be/lfaDB9h6StA
上の紹介動画を見ると、アクションゲームみたいに見えるのですが、 まったくそんなことはありません。運や確率は関係なく、 タイミングを狙って操作する必要もありません。反射神経は不要です。 Lara Croft GOは、 純粋に詰め将棋のように一手ずつ進めていく種類のパズルゲームなのです。
詰め将棋と便宜上書きましたが、そんなに複雑でもないし、 難しくもありません。よいゲームに見られるように、 難易度の調整が非常にうまく出来ており、 飽きもせず、行き詰まりもせず、 少しずつ進んでいけるようにできています。
このパズルゲームを解いているとき、 説明文の書き方に通じるところがあると思いました。 新しい要素は同時にたくさん出てこない(ここで伝えたいたった一つのこと)。 必ず一種類ずつ登場する。しかも、初登場のシーンでは、 その特徴がよくわかるようになっている(良質の例題)。 二回目に登場するシーンでは、 その特徴を生かした応用例が出てくる (理解したかどうかを調べる練習問題)。
たとえば「壊れかかった道」という場所がある。 最初は必ずそこを通らせ「二回通ると落ちる」 という情報がユーザにはっきり伝わる。 それは、実際に二回通ると穴に落ちて死ぬからだ。 その情報がヘルプなど見なくてもちゃんと伝わる(良質の例題)。
少し進むと「壊れかかった道」が壁として使われる。 その場面では「二回通ると落ちる」という性質をうまく使い、 「わざと二回通って落ちることによって、先に進む」 ということを自力で発見しなければならない (理解したかどうかを調べる練習問題)。 うまいなあ。
そのようなシーンを積み重ねながら、 ユーザはこのゲームの世界の複雑な成り立ちを、 少しずつ少しずつ理解する。 しかもばらばらの知識が増えるのではなく、 相互関係をつかみつつ。
そうして、次第に解くのが難しいシーンに向かうのだが、 そこでは、ここまで無理なく得た知識を自分なりに組み合わせて解く。 そして、うまく組み合わせれば自然に解ける。 この難易度バランスが絶妙なのである。 思わず「私ってすごい!私ってもしかして賢い?」 と自画自賛しそうになってしまうほどだ。
ということで、この"Lara Croft GO"、 いつのまにかコンプリートしていたのでした。
◆Lara Croft GO
http://www.laracroftgo.com
* * *
おもしろかったツイート(@tsujimotter さんによる)。
--------
「2は素数の中で唯一の偶数」っていうけど、
「3は素数の中で唯一の3の倍数」だし「5は素数の中で唯一の5の倍数」やで。
https://twitter.com/tsujimotter/status/639693716999958528
--------
確かにその通りですね。
「偶数」か「奇数」かという聞き方をすると何だか2が特別な感じがするけれど、 偶数のことを「2の倍数」と表現すれば、
・素数の中で、2は唯一の2の倍数
・素数の中で、3は唯一の3の倍数
・素数の中で、5は唯一の5の倍数
といえます。まったくその通り。一般に、
・素数の中で、pは唯一のpの倍数
ですね!
* * *
素数といえば、中学生のころ、こんなことを考えた。
出席番号が素数の人を考えよう。 素数なら2番でも11番でもいいけれど、その出席番号をpとする。
最初の番号1番から順にn人ずつのグループを作ることにする(nは2以上の整数)。 たとえば、n = 4なら、
1 2 3 4 で一グループ、
5 6 7 8 で一グループ、
9 10 11 12 で一グループ、
...
という具合。
ここで「出席番号p番の人」と「出席番号p+1番の人」が、 別のグループにわかれてしまうのは、 「p人ずつのグループを作った場合」(つまり n = p の場合)だけである。 それ以外の場合、p番の人とp+1番の人は、必ず同じグループになる。
たとえば、p = 5として、5番の人と6番の人は、 ほとんど必ず同じグループになります。5番と6番がわかれるのは、 「5人ずつのグループ」でわけたときだけ。
子供心に「おお!」と思ったのをよく記憶しています。
* * *
「同じ」について。
Webサービスなどで 「住所は全角文字で入力してください」と強制されるときがある。 つまり(メルマガで区別つくかわからないけれど)、 「3」じゃなくて「3」にせよということである。 プログラムを書いたことがあると、こういう強制は理不尽だと感じる。 なぜなら、ユーザに強制しなくても、 プログラムで自動的にどちらかに統一することは容易だからだ。
入力する形式を統一させたくなるのは理解できる。 同一のものを表す方法が複数あるとトラブルになりやすいからだ。 たとえば、あるデータの所番地が「3丁目(半角)」と書かれていて、 別のデータの所番地が「3丁目(全角)」と書かれているために、 同一の所番地と判断できなくなってしまうことが起きる。 だから、同一のものは形式も同一に揃えておき、 毎回必ず同じ表現になるようにするほうがいい。
『数学文章作法』にも書いたけれど、 文章を書くときの用語の選び方でも同じことがいえる。 同一の概念を表す用語が何通りもあると、 読者は「この用語とあの用語は同じ概念を表しているのか?」と迷うことになる。 これは困る。用語統一は大事な作業だ。
ところがおもしろいことに、説明文を書くときには 「同一のものを複数の方法で説明する」のが有効である。 用語は同一のものを使うのだけれど、 インフォーマルに説明してからフォーマルに説明する。あるいは、 図で見せてから文章で解説する。そのようにした方が理解が深まる。
同一のものを複数の方法で説明されると、 読者は自分の理解を確認し、 別の角度から同じものをとらえ直すことができる。これで理解が深まる。 それが成り立つのは「別な表現方法を使っているけれど、 これらは同じものを表現している」と読者がわかって読むからだろう。
ところが、二つのものが同じかどうかの判定方法がその表現だけだとつらい。 表現が一致すれば同じもの、表現が少しでも違えば別のもの。 そういう状況の場合には、同じものに別の表現をされてしまっては、 トラブルになるわけだ。それは当たり前のことである。
同じかどうかを判定するためには、判定の基準を定めなければならない。 言い換えると「いかなる意味でこの二つは同じなのか」を明確にするということ。 これは簡単なようで、とても難しい。 たとえば、「3丁目4番5号」と「3-4-5」とは同じか。 所番地だという情報があれば同じといえるかもしれない。
なぜこんなありきたりのことをくどくど書いているかというと、 ちょうどいま書いている『数学ガールの秘密ノート/ベクトルの真実』で、 同値関係を決めるという話題を校正しているからである。
「こっちのベクトルと、あっちのベクトルは同じだ」
「こっち、あっちと場所が違うのに、なぜ同じ?」
「同じ」とはどういうことかを定めることは、難しいけれど大事なことである。
* * *
結城はプログラムや原稿ファイルのバージョン管理にgit(ギット) というバージョン管理ソフトウェアを使っています。 先日、GitHubやBitbucketのようなサービスを利用するのではなく、 自分所有のサーバにリポジトリを作る方法を調べていました。
検索しているうちに、 Pro Gitという参考書がまるまる一冊Webで公開されており、 その日本語訳も作られているのを見つけました。
◆Pro Git
https://git-scm.com/book/ja/v2
調べたことをブログにまとめ、このWebサイトをTwitterで紹介したら、 このPro Git日本語訳をメンテしている方(@harupong さん) から「Pro Gitのご紹介ありがとうございます!」 とのリプライをいただきました。驚きです。
https://twitter.com/harupong/status/640471344337956865
この方は結城の『数学文章作法』の読者さんとのこと。 「訳文に迷ったときはいつも数学文章作法に助けてもらっています」 などと言っていただき、感激です。
こういうやりとりって、すごく嬉しいですね!
* * *
ツイートでのやりとりといえば。
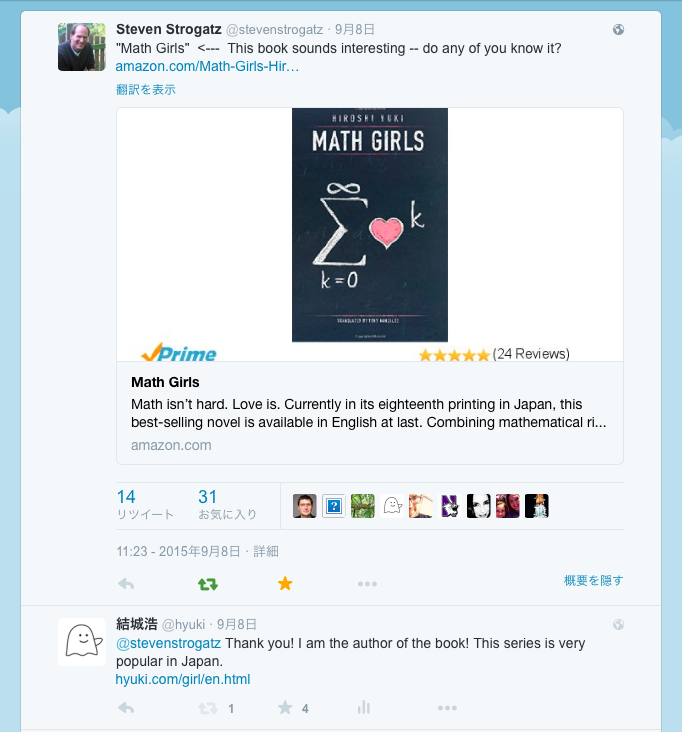
先日、Twitterで、著名な数学者のSteven Strogatz氏が"Math Girls" に興味を持ったというツイートをなさっていました。 緊張しつつリプライしたところ、 "congratulations - it sounds like a wonderful series of books!" という応援メッセージまでいただきました。
https://twitter.com/hyuki/status/641218043863937024
たいへんうれしいできごとでした。 さっと紹介できるように、英語版のWebページを作っておいてよかったです。
◆数学ガールの英語ページ
http://www.hyuki.com/girl/en.html
* * *
ベクトル本、先週は毎日一章ずつ見直していました。 積み残しもあるけれど、毎日一章というのはよいペースでした。
ばりばりと読んでばりばりと直す作業。 仕事が与えられているというのは、ほんとうに感謝なことです。 いつも喜び、たえず祈り、すべてに感謝して歩みましょう。
原稿に向かっていないときは「あそこが弱い」や、 「こっちも書けていない」という不安がよぎるものです。 でも、いったん原稿に向かって読んでいくと、 おもしろくてどんどん先に進んでしまいます。 これは原稿を直しているといつも起きる現象です。 不思議なものですね。
日曜日の夜に「明日は月曜日か〜」 といって憂鬱になる人は多いと思いますが、 いったん月曜日になり、火曜日を迎えると何とか過ごせるもの。 これもまた、いったんいつもの仕事に向かえば、 普通に進むことができるという同じ現象かもしれませんね。
だから、ぼんやりとした不安と戦ってはいけないのかもしれません。 「対処できる問題は何かを見つけること」 それから「対処方法を考えること」に力を注ぐ。 しっかり判断、淡々と実行。 自分の最善を尽くしたならば、安心して休息を取る。 それがいいのではないだろうか。
仕事にきちんと向かわず、 ぼんやりとした不安に無理矢理対処しようとすると、 労力は分散されるし、進捗も明確じゃないし、 残っている作業もよくわからない。 それでは不安も消えることはあるまい。
疲れているときや不安になっているときは、 自分の「できなかった部分」や「できていない部分」 に心が行きがちである。 「あれもこれもできてない……」ってね。
けれども、しっかりと「できた部分」にも目を向ける。 自分に正当な評価を与えた方がいい。 具体的には「自分をほめる」ということです。 特に「自分はだめだ」とばかり考えている人は、 もっともっと、自分をほめてもいいと思うのですよ。
あなたはどう思いますか。
* * *
それでは今週の結城メルマガを始めます。 今回は「フロー・ライティング」のコーナーで、
「世界が変わる第一歩」
という文章をお送りします。
どうぞごゆっくりお楽しみください!
目次
- はじめに
- フロー・ライティング - 世界が変わる第一歩
- メンツを守る
- エゴサーチで傷つかないか - Q&A
- おわりに