結城浩の「コミュニケーションの心がけ」2018年10月9日 Vol.341
はじめに
結城浩です。
いつも結城メルマガをご愛読ありがとうございます。
いよいよ今週末には『数学ガールの秘密ノート/行列が描くもの』が刷り上がり、結城は全国の書店に送られる《サイン本》を作る作業を行います。今週末から来週にかけて書店に並び始めることになります。
先週もお話ししましたが、正確に「何日にどこの書店に並びます」ということは結城にはわかりません。申し訳ありません!でも、公開できる情報はTwitterを中心にアナウンスしていきたいと思います。どうぞご理解ください。
《サイン本》や《メッセージカード同梱本》などの情報もアナウンスします。配本される書店さんのリストは、結城が入手できしだいTwitterやnoteなどでアナウンスする予定です。
◆『数学ガールの秘密ノート/行列が描くもの』
https://bit.ly/hyuki-matrix
いよいよです。ぜひ、応援よろしくお願いいたします。
* * *
おもしろい本の話。
ふと思ったこと。
「こういう本を書こう」としっかり考えて書くと、いい本ができる。
でも「どんな本になるかわからないけど、おもしろいからこれ書く!」みたいに突き動かされて書くと、ものすごくおもしろい本ができるのではないだろうか。
とはいえ、突き動かされて書いたものは独り善がりになることも多い。
また、ひととき燃え上がった情熱がすぐに冷めてしまって最後まで行き着かないことも多い。
それに、なにより「突き動かされる」という表現から自明なことだが、そんな状況はそもそも自分で制御できない。「よし、次の本は突き動かされて書こう!」なんて言えないよね。
せいぜい言えるのは「突き動かされて書きたい気分」になったときにそれを大事にすることくらいだろうか。
まるで、恋だな。
◆文章を書くのは、恋に似ている。
http://www.hyuki.com/dig/bunkoi.html
* * *
カメラで写真を撮ることとグラレコの話。
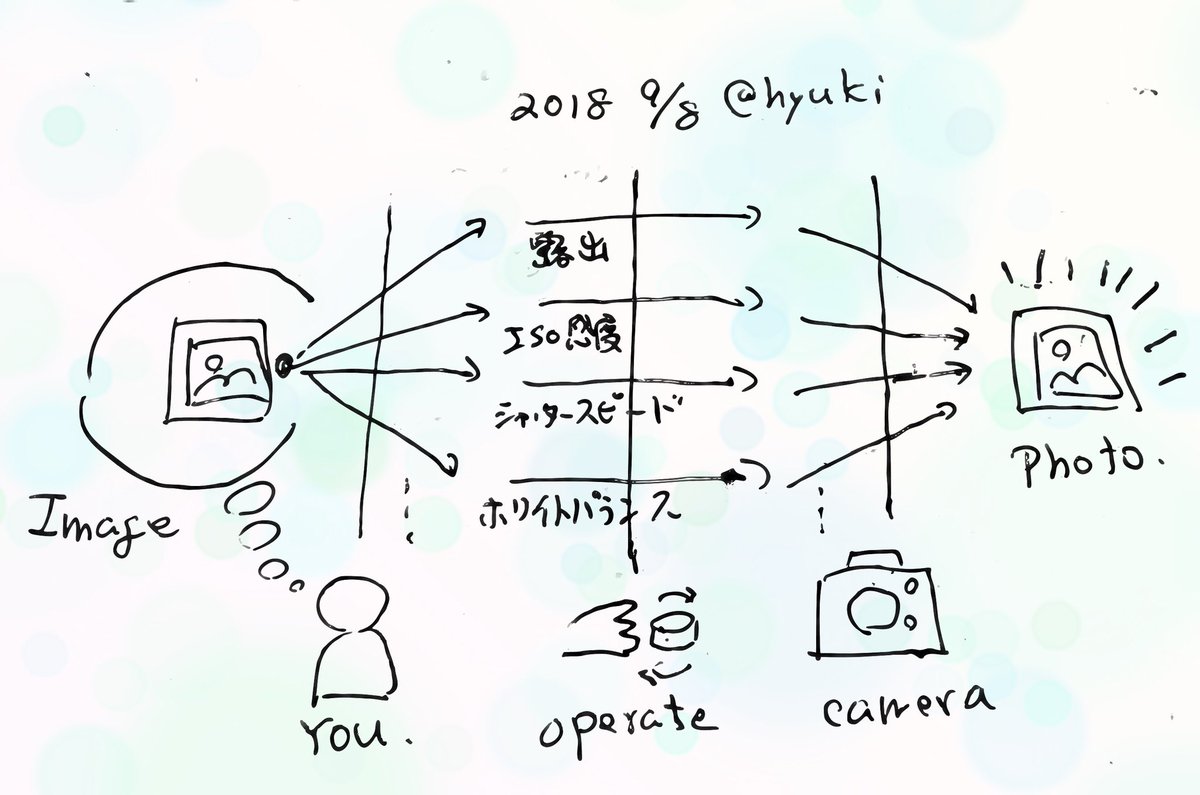
先日、朝の食卓で彼女(妻)が「カメラで写真を撮るというのはどういうことか」を結城に話してくれました。興味深く聞いていたのですが、聞いているうちに「グラレコ」(グラフィックレコーディング)したくなったので、手元にあった紙に描いてみました。これです。
自分が撮りたいイメージをパラメータに変換し、カメラを操作し、カメラが写真にする流れを描きました(写真の構図などは無視しています)。
左側には自分が思い描くイメージがある。撮影者はそれをイメージしながら写真撮影のためのパラメータを調整する。そのパラメータをカメラで設定する。そして撮影すると写真ができる。そのような流れです。
どうして結城がこういう図を描きたくなったかを自己分析してみました。どうも、たくさんの用語(露出、ISO感度、シャッタースピード……)が出てくると同時に、たくさんの存在(自分、カメラ、写真、イメージ)が出てきたからのようです。
たくさんの用語や存在が出てくると話がごちゃついてきますよね。何と何が同じレベルの用語なのか、何から何へどんな情報が伝わっていくのか、それらを整理しないことには頭にうまく入ってきません。それが気になったので図を描きたくなったというわけです。
図に描いていると、ものごとが整理されていくようすがよくわかります。カメラを学ぶことについて、こんなふうに思いました。
「カメラを学ぶというのは《自分の作りたいイメージをどのようなパラメータで表すか》を学ぶ側面と、《自分のカメラのどこを操作すればそれぞれのパラメータを設定できるか》を学ぶ側面があるわけなんですね」
図を描くことで整理する。それはとてもおもしろい感覚です。
* * *
学校で習ったかどうかの話。
「数学ガール」シリーズや、「数学ガールの秘密ノート」シリーズの読者さんからときどき「内容が中学や高校の範囲を越えている」という感想をいただくことがあります。「だから難しい」というニュアンスの場合もあるし、「だからおもしろい」というニュアンスの場合もあります。感想をいただけるのはありがたいことです。
作者として(あるいは一読者として)結城が思うことは、両シリーズに登場する彼女たちはおそらく「『中学や高校の範囲を越えている』という概念を越えている」のだと思います。彼女たちは、自分が知りたいと思うことを知ろうとし、考えたいと思うことを考えている。そして気になることや疑問に思うことを質問しあっている。「学校で習った範囲かどうか」ということをそれほどは意識していないように思います。
たとえば文章を読んでいて、知らない言い回しが出てきたとき「これは学校で習った言い回しか」ということはあまり意識しないと思います。それよりも「これってどういう意味だろう」と考えますよね。人に聞いたり調べたり。それと同じことなんじゃないでしょうか。
「学校で習ったかどうか」はどうでもいいと言いたいのではありません。そうではなくて、「学校で習ったかどうか」はさておき、知りたいと思うことを知り、学びたいと思うことを学ぶことは楽しいですよと言いたいのです。「学校でまだ習っていないから知らなくても不思議ではない」というのは理解できます(これから学べばいいんだよということです)。でも「学校でまだ習っていないから知る必要はない」というのは理解しにくい態度ですね。
* * *
おもしろい本を読む話。
ある小説を読んで考えさせられた。時代考証いい加減で、論理的にも破綻していて、登場人物の行動は一貫性に欠けている。のに、めちゃめちゃおもしろい。設定がいいのかもしれないし、キャラが立っているからかもしれない。落ち着いて考えると話が大半破綻しているのだけど、おもしろくて最後まで一気読みしてしまった。
破綻していると思ったけど、表現には勢いがあるし、登場人物の書き分けもなされている。それがあるので完全崩壊は免れている。最もすぐれていたのはテンポだ。新しい事件がどんどん起こるので、登場人物はそれに必死に対処せざるをえない。スピーディ。登場人物がほっとする間もなく次の事件が起こる。読者は飽きる暇がない。
二回読みたいか、というと「うーん」とうなってしまうけれど。
* * *
ことわざの理屈っぽい解釈の話。
「帯に短し襷に長し」ということわざがあるということは「帯と襷の適切な長さ」を比較すると「帯>襷」だなあ、と思いました。
どうして「帯>襷」といえるかを理屈っぽく説明します。
「帯に短し襷に長し」というのは、ひも状の何か(たとえばそれをXとしよう)を見たときに「帯にするにはXは短すぎるし、かといって襷にするにはXは長すぎる」という感覚を利用して「中途半端」を表現したことわざですね。つまり、帯>X>襷ということ。ですから「帯>襷」となります。
ちなみに「帯に短し襷に長し」の英語訳をさくっと検索してみると「帯>X>襷」的なニュアンスの表現はほとんどありませんでした。そういう不等式ではなくて「Xは帯にできないし、Xは襷にもできない」という否定された等式のような表現が多かったですね。たとえば「X is good for neither 帯 nor 襷」といった表現です。適切なものの集合をSとして「∀C∈S(C≠X)」みたいな表現もありました。
だから何? という主張は特にありません。単にことわざを理屈っぽく解釈したかっただけでして……
* * *
「トリカラ」は鳥の唐揚げ。では「ヒトカラ」は何だろう。
「ヒトカラ」は一人カラオケ。では「トリカラ」は何だろう。
* * *
ライブコーディングの話。
Rui Ueyamaさん(Googleのソフトウェアエンジニア&スタンフォードの学生)が、簡単なプログラミング言語を作るコーディング動画を公開しています。プログラムを少しずつ大きくしていくようすを解説つきで紹介しています。C言語を使ってプログラミング言語処理系のプログラムを作っているようすを「ライブで」見ることができます。
プログラミングに関心があるなら、たいへん楽しめると思います。途中でマニュアルを調べ出すようすも動画に登場しますよ。
◆簡単なプログラミング言語を作るライブコーディング
https://twitter.com/rui314/status/1040247100238262272
結城も若い頃、こういう感じで「小さなプログラム」をどんどんふくらませていくプログラミングをよく行いました。とても楽しいんですよ!
* * *
それでは、今回の結城メルマガを始めましょう。
どうぞごゆっくりお読みください。
目次
- 大学レベルの数学を学びたいとき、まず何から? - 学ぶときの心がけ
- プログラミングを始めて2ヶ月、iOSアプリを作りたいが進展がない
- 受験生、気付く力を養うには - 学ぶときの心がけ
- ひらがなは読みやすいか - 文章を書く心がけ
- 「とりあえずやれ」が苦手です - 仕事の心がけ
- いまは亡き母に会いたい
大学レベルの数学を学びたいとき、まず何から? - 学ぶときの心がけ
質問
大学レベルの数学の勉強を始めたいです!
まずは微分積分から手を付けた方がいいでしょうか。
回答
ご質問ありがとうございます。
あなたが興味があるところ、自分の力に合うところから始めて構わないと思います。
特にこれというのがなければ「論理と集合」という分野から学ぶのもお勧めできます。
なぜ「論理と集合」をお勧めするかというと、これからどのような数学の本を読むにせよ、論理と集合が必ず出てくることになるからです。
こちらのページで紹介している『論理と集合から始める数学の基礎』という本を推薦します。
◆嘉田勝『論理と集合から始める数学の基礎』
https://math.hyuki.net/20180513225240/
この本は数学で出てくる数式や言い回しなどについての説明もありますので、今後あなたが数学の本を読んでいく上での基礎力をつけるのに大いに役立つと思います。
ただし、小説を読むみたいにさささっと読む本ではありません。頭をフルに使ってしっかりと考えながら読む本ですので、その点はご理解ください。
ご質問ありがとうございました。