結城浩の「コミュニケーションの心がけ」2015年12月8日 Vol.193
はじめに
おはようございます。 いつも結城メルマガをご愛読ありがとうございます。
最近はすっかり「冬」になりましたねえ。 晴れた天気ならばよいのですが、 曇っていたり、風が強かったりすると、 ちょっと「ふにゃあ」とめげてしまいそうになります。
それに「朝のおふとん」の誘惑に負けないのは難しい。 つい「あと五分寝させて」という気持ちになってしまいます。 こんな絵を描きたくなるくらい。
ま、まあ、それはそれとして、 毎日の生活の中に「小さな楽しみ」を見つけて、 元気に過ごしていきたいですね。
* * *
「よかった探しリース」の話。
結城は毎年、クリスマスシーズンに「よかった探しリース」 というWebの企画を行っています。 個人のサイトやブログなどをリンクでつなぐことを、 クリスマスの「リース」に見立てる企画です。
そしてそれぞれのページは、
「今年よかったことを探そう」
という共通のテーマで結ばれています。
毎年実施して、今年で19回目になりました。 もしよければ、あなたも参加してみませんか? こじんまりした企画ですので、どうぞお気軽に!
◆よかった探しリース
http://www.hyuki.com/ring/
* * *
「もこもこ」の話。
最近、調子が悪いというのではないけれど、 あれこれ考え込んでしまい、 うまく言葉にならない「もこもこした気持ち」 になることがあります。イメージ図に描くと、 こんな感じ。
Twitterで @tatesuke さんから、こんなリプをいただきました。 「スレッドお化けの触り心地はどんな感じなんでしょうね。 ふわふわなのかもこもこなのか。 個人的には中は空で、風で膨らんでいるカーテンみたいな感じを想像していますが」
◆ふわふわ?もこもこ?
https://twitter.com/tatesuke/status/667525008156049409
結城は、スレッドお化け坊やのさわりごこちは、 「触れる相手によって感触が違う」んじゃないかな、 と想像しています。
おもしろいもので、誰か自分以外の人と、 こういうちょっとしたやりとり(おしゃべり)をするだけで、 何だか晴れやかな気分になりました。
ひとりで考え込みすぎるのは、 あまりよくないのかもしれません。 誰かと何ということもない対話をするのは、 意外に大事なことなのかも。
* * *
数学の話。
結城は、ときどき数学の問題を出します。 先日はTwitterのアンケート機能を使って、 こんな問題を出しました。
π度と1ラジアン、大きいのはどっち?
アンケートは24時間で締め切られ、 結果はこんなふうになりました。
◆π度と1ラジアン、大きいのはどっち?(スクリーンショット)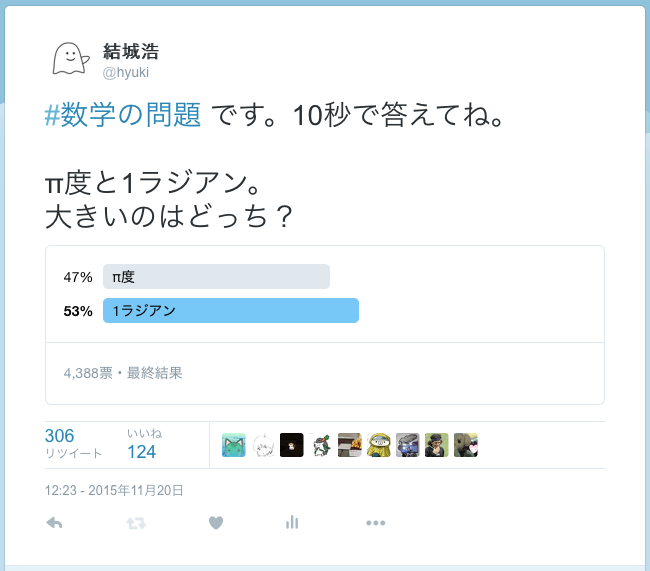
正解は、1ラジアンです。
πは3.141...という数ですから、 π度というのは3.141...度ということになり、 「3度」よりも少し大きい角度です。
ラジアンというのは、その角度に対する円弧の長さが、 円の半径の何倍になるかを表したものです。 ですから、360度は2πラジアンに等しく、 また、180度はπラジアンに等しくなります。 なので、1ラジアンというと「60度」よりも少し小さく、 約57度ほど。
ということで、1ラジアンの方がずっと大きいことになりますが、 先のアンケートでは意外にまちがいが多かったですね。
通常「ラジアン」という角度の単位は、πや2πやπ/2など、 πと合わせて使うことが多いものです。 なので「1ラジアン」はどれくらいかを考えることは少ない。
一方「度」という角度の単位は、30や45や90や180など、 整数で使うことが多いもので「π度」を扱うことは少ない。
結城はそれを考えてわざと「π度と1ラジアン」 を比較させる問題を出題しました。 でもそれは「引っ掛け」という意味ではなく、 「1ラジアン」のおおよその大きさを体感的に知っているかどうか、 それを確かめたかったからです。
実際、ある数学の先生からは「1ラジアンがだいたい何度か」を問うのは、 ラジアンを教えるときには定番の問題だとあとから教えてもらいました。
他にも数学の問題をいくつか出したので、 また、後ほどお話しします。
* * *
スクリーンショットの話。
ふだん仕事でコンピュータを使っているとき、
「いま見ているこの画面を保存しておきたい」
というのはよくあることです。 いわゆる「スクリーンショット」を撮るということですね。 先ほども、アンケート結果のスクリーンショットをお見せしました。
結城はMacでスクリーンショットを撮るツールを三つ使っています。
一つは、Gyazoです。これはスクリーンショットを撮影して、 即時にサーバにアップロードして共有できるというもの。 結城はこのツールの中に含まれているスクリプトを改造して使っています。
◆Gyazo
https://gyazo.com/
もう一つはSimpleCapです。ドラッグして範囲指定することもできるし、 前もってサイズを定めておくこともできるので、たいへん便利です。
◆SimpleCap
http://xcatsan.com/simplecap/
そしてもう一つはEvernoteクリップです。 スクリーンショットで撮った画像をすぐにEvernoteに保存できるので便利。
参考資料をMacで読んでいるとき、
「あ、ここ、あとで再読しよう」
「この部分はあの本を書くときに参考にしよう」
という部分を見つけたら、さくさくとスクリーンショットを撮り、 Evernoteに保存するようにしています。これは非常に有効。 Evernote上に自分専用の参考書を作るようなものだからです。
そういえば、先日「液晶画面をカメラで綺麗に撮る話」が話題になっていました。 ひとことでいえば「カメラを少し斜めにして撮る」のだそうです。 おそらく画面とカメラで、ピクセルが干渉しないようにするためなのでしょう。
◆液晶画面をカメラで撮るときに出るモアレを消す
http://togetter.com/li/901190
* * *
日常生活の中での発見の話。
以下のリンク先は、高等学校の塚本浩司先生が、 生徒が発見したなにげない現象を解明していくという論文です。 まるで、探偵が犯人を追い詰めていくような、 そんなどきどきするお話になっています。
◆コーヒーカップとスプーンの接触音の音程変化
http://ci.nii.ac.jp/naid/110007491429
上のリンクに書かれていたアブストラクトを以下に引用します。
---------
マグカップでインスタントコーヒーを溶かしてかき混ぜるときに,
ティースプーンとマグカップがぶつかり,音が生じる。
この音は,インスタントコーヒーが完全に溶解するまでの間,
音程が「くぐもった低い音」から徐々に甲高い音に変化する。
周波数特性を行ってこの現象の原因を解明し,その過程を教材化した。
この教材は,音波・音響や振動に入門する教材にもなりうるが,
それ以上に,科学研究の手法を学び,
物理学を身近に感じるために最適の教材となりうる。
---------
現象から仮説を立て、それを検証していくという、 まさに、科学的研究の王道を行くような論文です。
この論文は、以下の @qutrit_a さんのツイートで知りました。
https://twitter.com/qutrit_a/status/668247116477833216
* * *
文章を書く人が一人いると、 それを喜ぶ人が九九人いて、文句言う人が一人いる。 文句言う一人のために書くのをやめてはいけない。
人気が出て、喜ぶ人が九九万人に増えたら、 文句言う人は一万人に増える。 それでも、書くことをやめてはいけない。
* * *
CodeIQの話。
結城は現在CodeIQというサイトで、 「マヨイドーロ問題」というプログラミングの問題を出題しています。
先週の木曜日から公開されたのですが、 週明けの月曜の朝の時点ですでに300人以上の人が挑戦しています。 ありがたいことです。
◆結城浩の「マヨイドーロ問題」
https://bit.ly/c19mayoi
今回は一年ぶりの出題になるので、 少し趣向を変えて「自動採点問題」にしてみました。 つまり、解答者がプログラムを送信すると、 即座に正解/不正解が判定できるという方式です。
この方法だと、解答者は何度でも挑戦できますし、 自分の頭に情報が残っているうちにフィードバックを受け取ることになるので、 より楽しくチャレンジできますね。
それはそれでけっこうなことなのですが、 出題者としてはいささか緊張感が高まることになります。 つまり、自分が用意する「正解」がほんとうに正しいかどうか、 前もって確信を持って用意できなければいけないからです。
あたりまえのように聞こえるかも知れませんが、 実はあたりまえではありません。
昨年結城が使っていた方法では、解答者の投稿をすべて受け取り、 〆切が過ぎてからフィードバックを(半手動で)行っていました。 つまり、解答者がどんな解答を行ったかを、 フィードバック「以前」に見ることができたのです。 多数の解答者の答えを見ることで、 結城自身が用意した「正解」がほんとうに正しいかを確認できたという意味です。
しかし、今回のような自動採点の場合にはそれができません。 結城が一人で「私の用意する解答は絶対に正しい」と確信できるほど、 準備を整えなければならないのです。
それは、問題を出す立場としてはある意味当然の準備になるわけですが、 なかなか緊張するものではあります。 しかし、その反面、実際に問題がオープンされ、 多くの人が正解を出し始めると、 結城は出題者として大きな満足感を得ることになります。
プログラミングに慣れていない人は、 自分の書いたプログラムが「動くかどうか」が最初の課題となります。 でも、実はプログラムが動くかどうかというのは、 ある意味ではやさしい課題です。 なぜかというと、動かなければ、 動かないことが「すぐわかる」からです。 エラーになりますからね。
それに対して、それらしい結果が出たときに、 それが「ほんとうに正しいのか」を判断することは難しい。 とっても難しい。
その難しさというのは哲学的な意味合いも帯びる。 なぜかというと、プログラムを使って解く問題というのは、 おうおうにして、
「非常に規模が大きいため、
人間が実際に試すことができない問題」
だったりするからです。
人間が実際に(たとえば手計算で)試すことはできない。 プログラムを使ってはじめて得られる答えが目の前にある。 さてさて、これは、正しい答えだろうか。
そして、もしもプログラムを経ずして正しい答えだといえるなら、 プログラムを使う意味はどこにあるのか。
そういう意味で「プログラムの出す結果が正しいか」 という判定は非常に難しい問題をはらむのです。
そんなことを考えつつ、CodeIQの問題を作っています。
* * *
レトリカル・クエスチョンの話。
レトリカル・クエスチョン(修辞疑問)というのは、 疑問の形をしているけれど、その真意は疑問ではないという文です。
「どうして、こんなことしたの?」
というのは疑問の形をしていますが、 叱責であることも多いですよね。 答えを知りたくて聞いているのではなく、 怒っているだけ。
ちょっと意識すると、 レトリカル・クエスチョンは日常生活のあちこちで見つかります。 自分自身が使うときもあるし、 他の人が使っているのを耳にすることもあります。
先日ファミリーレストランで、 小さな子供が飲みものをひっくり返したとき、 親が、
「どうしてちゃんと押さえてないの?」
と叫んでいました。 これも、レトリカル・クエスチョンの一種ですね。 別に押さえていない理由を知りたいわけではない。 親は「ちゃんと押さえなさい」と怒っているのです。
レトリカル・クエスチョンは叱責になるとは限りません。 子供の歌で、
どうしてお腹が減るのかな?
ケンカをすると減るのかな?
というものがあります。あの歌も、歌詞を注意深く読んでみると、 レトリカル・クエスチョンであることがわかります。 「お腹が減る理由」を知りたいというのは真意ではなく、
おかあさん、おかあさん。
お腹がすいたから、何か食べるものちょうだい!
という歌なんだよな、と思います。
仕事でレトリカル・クエスチョンが飛び交うのは考えものですが、 日常生活においては、微妙なニュアンスを出し、 ときにはいい効果を上げる場合もあります。
あなたのまわりには、 どんなレトリカル・クエスチョンがあるでしょう。
* * *
それでは、今週の結城メルマガを始めます。 今回は、いつもの読み物の他に、
「誤読は著者の責任か?」
というQ&Aをお届けします。そこでは、 『エンジニアとして世界の最前線で働く選択肢』 という書籍の著者、 竜盛博さんとのメールのやりとり全文を書きました。
◆『エンジニアとして世界の最前線で働く選択肢』(竜盛博)
http://www.amazon.co.jp/gp/product/4774176567/?tag=gnk-22
どうぞ、ごゆっくりお楽しみください!
目次
- はじめに
- 子育てと「夫婦の一致」
- 誤読は著者の責任か? - Q&A
- 数学の問題
- おわりに



