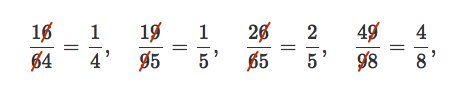結城浩の「コミュニケーションの心がけ」2017年9月12日 Vol.285
はじめに
おはようございます。結城浩です。
いつも結城メルマガをご愛読ありがとうございます。
＊ ＊ ＊
まちがっているのに正しい約分の話。
筑波大学の三谷純先生（@jmitani）がこんなツイートをしていました。
--------
Book of Curious and Interesting Puzzles で紹介されていた、
やりかたが間違っているけど、なぜか答えは正しい約分の例。
https://twitter.com/jmitani/status/901083528611323909/
--------
どういうことかというと、 たとえば「64分の16」という分数を考えます。
16/64
分子と分母の両方に6という数字があるので、 それを「約分」のように消してしまうのです。 すると、分子と分母から6が消えるので、
1/4
という形になりますね。そしてこれはたまたま、 16/64を正しく16で約分したときと同じ結果になるのです。 約分のやり方としてはまちがっていますが、 結果的には正しくなっちゃうという分数なのですね。
おもしろいです！
三谷先生のツイートでは、 同じ特徴を持つ3個の分数が紹介されていました。 それは、
16/64 = 1/4
26/65 = 2/5
19/95 = 1/5
の3個です。
これを見たとき、
「おもしろいけど、これで全部なんだろうか？」
と結城は思いました。
二桁分の二桁という分数に限るなら、 分子と分母にくる可能性があるのは10〜99ですから、 すべての組み合わせを試したとしても、大した数ではありません。
とはいえ手でやるのはめんどうですから、 さっそく小さなプログラムを書いてすべてを探してみました。 具体的には、
(10a+b)/(10b+c)
という形をした分数を探すということです。
プログラムを書き始めてすぐに「約分した結果1になる分数」 の存在に気づきます。たとえば、
22/22
は 1/1 になってしまいますよね。 そういうのはつまらないので除外しました。 そうすると「二桁分の二桁」で値が1になるもの以外は、 全部で4個あるようです。三谷先生が書いたものを除くと、 最後の1個は、
49/98 = 4/8
です。でもこれはさらに約分できてしまうので惜しいですね！ 何が「惜しい」のかよくわかりませんが（苦笑）。
ともあれ、見つかった分数は以下の4個です。
◆まちがった約分なのに、なぜか正しくなる分数（画像）
Rubyで書いたプログラムは以下で公開しています。
◆まちがった約分なのに、なぜか正しくなる分数
https://gist.github.com/hyuki0000/a9670b7a7b42554412e0111903635fc8
こういうプログラミングは、何かの「役に立つ」わけではありません。 でも、なぜか楽しいものです。自分が抱いた素朴な疑問である、 「これで全部なんだろうか？」 に対して答えを与えてくれるからでしょうかね。
＊ ＊ ＊
フォロワー数の話。
先日、結城をフォローしてくださる方が3万9千人を越えました。 多数のフォロワーさんに感謝です。
ところで、高校生になる息子がこんなことを言ってきました。
ねえ、お父さん。
お父さんをフォローしてる人って多いんだよね。
ぜんぶで 500万人 くらい？」
息子に言いたい。
私は、きゃりーぱみゅぱみゅさんではないのだよ……
※きゃりーぱみゅぱみゅさん（@pamyurin）のフォロワー数は、現在500万人強です。
＊ ＊ ＊
それではそろそろ、 今回の結城メルマガを始めましょう。
どうぞ、ごゆっくりお読みください！
目次
- はじめに
- 再発見の発想法 - Backtrack（バックトラック）
- テキスト作成エコシステム - 文章を書く心がけ
- 自己満足から逃れるには - Ｑ＆Ａ
- 自由に選択できるということ
- おわりに
