-
[S]道の駅の地元野菜やフルーツの見る目が少し変わる話
2014-01-22 00:3032pt今日は火曜ですが、気楽に始める[S]で。明日水曜日は通常にします。 さっき、録画してあったNHKの 地球ドラマチック「フルーツハンター~未知の果物を探せ~」 を見ました。 バナナの単一栽培が取り上げられていました。現在輸出されるのはキャベンディッシュ種一種ですが、遺伝的多様性に乏しく、病気が発生すると一気にやられる可能性があります。実際、以前はグロスミッチェル種というのが流通していましたが、パナマ病という病気で壊滅しました。キャベンディッシュ種にも病気が発生し、危機ではないかと言われています。 したがって、遺伝的多様性が重要であるということで、バナナでの品種改良の取り組みが紹介されていました。 他にもマンゴーでの取り組みが紹介されていました。(確か)アメリカの研究者が東南アジアの原野に踏み込み、原種を見つけてなんとか持ち帰って栽培に挑戦するというものです。また現地の市場に色とりどりに並ぶ果物を見て調査するとか。 すべて、素晴らしい取り組みで番組も面白かったのですが、カナダで作られたという世界をまたぐその番組を見ている間、日本ではそれら一つ一つが、日本の国土の中で起こっていると気付きました。日本では地元の品種を日本人自身が守り育て、地域で消費しているのです。 たとえば、私の住む瀬戸内は柑橘類の栽培が盛んです。 -
毎年東京から全国1700の市町村に移り住む様子がロングテールだった。(その1)
2014-01-21 01:0032pt(タイトル変えました。 2014/1/21)
先日47mapsというサイトを使って、日本の国土の25%に人口のたった2%しか住んでいないという地図を作りました。 最近、都会から地方への移住についての記事を考えていたので、47mapsでなにか見てみようと思い弄り始めたら、作った最初の地図が大変印象的なものになりました。 それがこれです。
これは、2012年の全国各市町村の東京都からの転入人数を示しています。転出は差し引いていません。47mapsのサイトで直接見ることもできます(注意:1700以上の自治体を描画するので描画が完了するのにとても時間がかかります)。 黒は 0人 青は 1人から 9人 緑は 10人から 99人 黄は 100人から 999人 赤は 1000人から 9999人 白は 10000人以上を示しています。 元は総務省の住民基本台帳人口移動報告というデータです。私も入手しましたので、以下それを参照しながら説明します。 まず1万人以上の白は東京付近のみにあります。東京23区、横浜市、川崎市の3都市です。 さて、この地図を出したときなんといっても驚いたのは、黒が少ないことです。生データを見ると、32市町村だけです。その他の全国1706市町村には、2012年の年間に少なくとも一人は誰かが東京都から転入しています。割合にして、98%以上です。まったく予想外でした。 2012年に東京都から都外へ転出した人は、合計約34万6000人です。東京都の人口は約1320万人で、2.6%、つまり転出している人は、3%弱なのですが、その3%弱の人々は、ほぼくまなく全国に移り住んでいるのです。ちなみに東京から福山に越した私は黄色組です! 比較のために、同様の地図を大阪府と愛知県で作ってみました。 -
「平等なウェブ世界」は終焉するのか
2014-01-18 01:0032ptこの記事にインスパイアされました。 「PCの死」と「平等なウェブ世界の終焉」 スマートフォンやタブレットの普及に伴いPCの出荷台数は大きく減少していますが、それに従ってウェブの世界も終わってしまうのではないかという考察です。スマートフォンやタブレットはアプリ中心で、ウェブを見る機会はどんどん減っています。そのままウェブは死んでしまうかもしれません。 ハイパーリンクされ、誰でもいつでもどこからでも平等かつ自由に利用できるワールド・ワイド・ウェブは徐々に消えていくだろう。その代わりデジタル世界は、より自己完結性の高い個々のアプリのドメイン内で生じることになる。
ということなのですが、本当に終焉するのでしょうか。 「ロングテール」の観点から考えると、それはあまり現実味がないように思えます。 今見てみたら私の iPhone には 162 個のアプリがインストールされていました。そのうち頻繁に使うのは10個弱、たまーに使うのはせいぜい数十、あとのアプリは事実上もう使っていません。世にはアプリが無数にありますが、その無数のアプリにアクセスする頻度はいくら集めても、良くアクセスするアプリの頻度には叶わないでしょう。 一方ウェブではハイパーリンクを介して無数のサイトにシームレスに繋がっており、またグーグル検索を介しても繋がっています。 -
心の底から「頑張れ!」と言えるようになりたい
2014-01-16 23:4532pt安易に「頑張れ」と言ってはいけないって言うじゃないですか。私も昔から、そうだよね、と思うのでなるべく言わないようにしていたのですが、どうにも腑に落ちなくて、悶々としています。それは、たとえば「代わりになんと言えばいいか」ということなのかと思って、いろいろ考えるのですが、その場その場で「これだ」というのを思いつく訳でもありません。もちろん検索すればその手の話はいっぱいアドバイスがあって、読んだ時は「そうだよね」とは思うのですが。 最近、象徴的な場面がありました。小学校のマラソン大会です。子供達が走る中、親達応援する人は「がんばれ〜〜〜」と盛んに声をかけます。そんなときはなんて言えばいいんだろうとその場で考えてみました。英語だと "You can do it!" とか言うみたいだし、たとえば「その調子その調子!」とか言えそうです。 でも、そう言ってもいいけど、道ばたの全員が「頑張れ!頑張れ!」と声援している雰囲気は別に悪くなく、自分も「頑張れ〜〜」と声をかけました。子供達も全員じゃなかったかもしれないけど、応援されてより力湧いてるように見えたし。 古いCMに、父親(松木安太郎)がサッカーをする息子にひたすら「走れ!走れ!」と声をかけ続けるのがあります(2005年だったそうです)。
当時もうるうるしたけど、今見てきたら、やっぱりうるうるします。タグは「ふざけたCMですね!(泣)」とか「なんなんすかこれ(涙)」とか、きっとうるうるするのは私だけではないはず。 松岡修造は特別な存在ですが、彼の激熱エール、見てて悪い気になる訳でもありません。 「安易に『頑張れ』と言ってはいけない」のかもしれないけど、逆に正しいタイミングなら心の底から「頑張れ!」を伝えられるのではないか?と思うようになったのです。 それはいったいどんな時なのでしょうか。 そう考えたとき、昔似たようなことがあったのを思い出しました。 中学生から高校生だった頃、「かわいそう」という言葉が大嫌いでした。ちゃんと相手の気持ちも理解してないくせに、薄っぺらい同情なんてかえって迷惑やんけと。そしたら「同情するなら金をくれ」の家なき子とかあって、やっぱそうじゃんねとか。後「大丈夫?」とかも。 -
[S]短時間睡眠、立体を伝えるテーブル
2014-01-15 23:0032ptいつもとちょっと違う水曜、今回は気楽に書き始める記事[S]です。 もう先月のことなのですが、こんな記事を読みました。 世界初の睡眠コントロールで1日2時間睡眠を可能にする「Neuroon」 - GIGAZINE 人間は毎日、夜から朝にかけてまとめて眠る「単相睡眠」という睡眠サイクルを持っていますが、動物は1日に複数回睡眠する「多相睡眠」を行っています。世界初の多相睡眠コントロールシステムによって多相睡眠のサイクルを可能にし、30分睡眠を1日4回行うだけでパワフルに1日中動くことができる効率的な睡眠をもらたしてくれるアイマスクが「Neuroon」です。
この記事を最初に読んだときは、こう感じました。「昔だったらすっごく興味持ったけど、今は小3、年長の子供もいて、自分も含めて規則正しい生活しないといけないから、ちょっと関係ないな〜」と思い、そのまま読み流したのです。 でもその後こんなツイートを見かけてはっとしました。
世界初の睡眠コントロールで1日2時間睡眠を可能にする「Neuroon」 http://t.co/vZwjALZDIH 何これ欲しいw実際に効果があるなら、産後に睡眠時間がとれなくて精神的にヤバくなってるママの救世主になるね。
― mai (@crystalforest) 2013, 12月 5
確かに。私の連れも子供が生まれたばかりの頃は睡眠不足で本当に辛そうでした。これ使ってちょっとでも睡眠の質が向上するなら、ほんとに救世主です。開発者はギークな感じの人ですが、新生児の母さん向けも意識しているといいです。 さて、もう一つ。話は全然飛びますが、これ驚きました。ちょっと古い話題なんですが。 MITが開発した立体を伝えるモーフィング・テーブルが凄く面白そう - おたほー (この画像は、Incredible video of the magic morphing table that lets you touch thingsという記事から。)
-
オーストラリアの一人あたり面積はとてつもなく偏っていた
2014-01-14 23:3032pt【ミラフツ名物ロングテール記事一覧 - NAVER まとめ】
アメリカの一人あたり面積もロングテールだった〜ロングテール解析法大公開〜の続きです。全ての元凶オーストラリアのデータも手に入りました! この話題、もともと、オーストラリアのこの地図がきっかけで調べ始めました。
この黄色い部分に人口の2%しか住んでいないというのです。 日本、そしてすぐデータの手に入ったアメリカについて、国民それぞれが住む場所の人口密度のデータを入手し、偏り方を調べました。 となるともともときっかけになったオーストラリアについても知りたくなります。無事見つけることができました。統計用に全国を 2196に分割したStatistical Areas Level 2 (SA2) と呼ばれる地区それぞれについて、人口や人口密度が掲載されていました。 早速見てみましょう。人口密度から一人あたりの面積(逆数)を計算し、一人あたり面積の大きい人から順に並べてその面積をグラフにしたのがこれです。
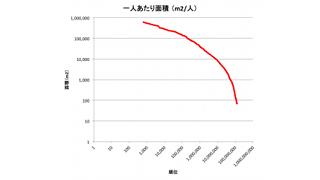
…とこれでは「わけがわからないよ」なので、目盛りを10, 100, 1000, ... と対数にしたのがこれです。
なんと、一人あたり面積が 1,000,000,000平方メートルつまり、1,000平方キロメートルを超えている人がいます。縦横 32km の広さに一人。各国一番狭いところでは100m2を切ってきますから、1千万倍以上の開きです。仮に所得でこの差を考えると年収10万円と1兆円! ちなみに、SA2で総数2196に分割された地区の中には人口0の地区が36あり、その総面積は約13,000m2、なんと日本4位の長野県(約13,600m2)と5位新潟県の(約12,600m2)の間です……。 横軸を普通に戻したのがこちら。
曲線の姿は日本、アメリカとはかなり違ったものになっています。オーストラリアとアメリカを比べると上位1割ではオーストラリアのが広く、下位9割の大部分ではアメリカが上です。さらに40%辺りでは日本とほとんど変わらないと、抜きつ抜かれつの大デッドヒートです。(苦笑 次に一人あたり面積の大きい人から、その面積の累積するとこのようになります。
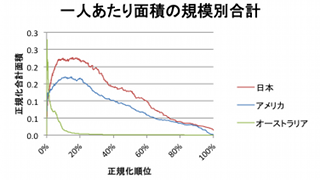
これは、なんと、オーストラリアの 2% 人口のところは約90%になっていて、つまり、人口の残り98%は国土の10%に住んでいることになります。対するアメリカは国土の50%、日本は国土の67% に住んでいるのに対して圧倒的な違いです。 さすが、冒頭の印象的な地図と共に記事として紹介されることはあります。 (注:以前は画像から分析して75%と書きました。値がかなり違いますが、国土を2196 に分割しているこの例よりはるかに少ない数に分割していることによると思われます。日本は75%と書きました。それは市区町村の人口順で求めたからです。人口密度で並べればよりシビアになります。) さらに前回紹介した「規模別合計」を見てもその違いは際立ちます。「規模別合計」は、ロングテール分布の特徴を調べるのに好都合です。なお、「規模別合計」については、改めて本家で式を用いた解説をしましたので、興味ある方はそちらを参照してください。 ロングテールを調べるのに便利な「規模別合計」の数学的解説この「規模別合計」を各国の一人あたり面積で行ったものが次になります。
日本・アメリカはじわ〜っと全体に広がっていて、いかにもロングテールな感じですが、オーストラリアは面積が広い方に極端に偏っています。さすが2%の人口で国土90%を占めてしまっているだけのことはあります。 明確な基準があるわけではありませんが、有り体に言って、オーストラリアはロングテール分布と言えないくらいの偏りだと思います。同じ「一人あたり面積」という統計で、国が違うことで分布の性質がここまで違うという例は少ないので、いろんな国で見ると極めて興味深い結果が出るのではないかと思います。 -
アメリカの一人あたり面積もロングテールだった〜ロングテール解析法大公開〜
2014-01-10 23:0032pt【ミラフツ名物ロングテール記事一覧 - NAVER まとめ】
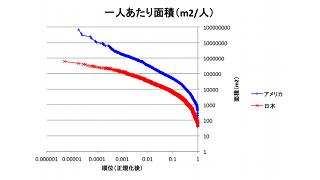
市区町村別一人あたり面積をプロットしたらロングテールだった の続きです。 市区町村別の人口密度から一人あたり面積を計算して、面積が大きい人からずらっと全人口分並べてプロットするとロングテールになってたという話でした。グラフを再掲するとこちら。左右同じグラフで、軸の目盛りの取り方が普通(左、リニア)と対数(右、1,10,100,..)になっています。
で、当然他の国がどうなっているか気になるわけで、さっそく直接アメリカの国勢調査のサイトに行ったのですが、データが州ごとに分かれているのしか見つけられず、うーと はまった後、おとなしく日本語でググったら、アメリカ・人口密度ランキング(郡別)というそのものズバリのベージがすぐに出てきました。最初からググればよかった……。 ということで、アメリカの郡別(州より一つ下)人口密度から日本と同じように計算して一緒にしたのがこれです。
国民の数が違うので、順位を全国総人口で割った正規化した順位に揃えています。日本と一緒で、いやむしろ日本よりきれいなロングテールの分布をしています。 青線は全体的に赤線のはっきり上にあって、これはつまりアメリカ人の方が人口密度が低いということです。これは当然ですね。 一番右端を見ると、アメリカ37平方メートル、日本46平方メートルと同じような狭さになっていますが、アメリカの曲線は鋭く切り立っていて、つまりアメリカではその高度に過密な地区、たとえば1000平方メートル以下に住む人の割合がごく限られていることがわかります。それに対して日本の曲線の右端部分は滑らかです。これは順位の軸を普通(リニア)に戻すとよりはっきりします。
ご覧のように、右端の部分ではっきりと差が出ます。 アメリカでは約10%弱の人は特に高度に過密な地区に住んでいますが、日本では面積の変化はなだらかです。つまりアメリカでは、他の地区に比べてここは都会という違いがはっきりしているはずで、一方日本は、超大都会から地方都市までの街の込み具合の変化がなだらかで線引きが難しいでしょう。 元のグラフに戻りましょう。全体的な傾向を見るために、直線を入れてみます。
アメリカでは右端を除くと、とても直線的で傾きも急です。これは、いわゆるべき乗則と呼ばれる分布にかなり近い形です。 一方日本の方は、傾きが鈍いだけでなく、さらに全体的にたわんだ曲線です。 これは、大きな違いをもたらしますが、このまま説明するのは難しいので、新しいグラフを導入します。順位規模ごとの合計値を集計する
今例題として、次のような状況を考えます。 ミラフツ県には、 一人あたり面積 10,000m2 のところに 1人住んでいる。 一人あたり面積 1,000m2 のところに 10人住んでいる。 一人あたり面積 100m2 のところに 100人住んでいる。 このとき、各面積の人が住んでいる総面積はどれも、10000×1 = 1000×10 = 100×100 = 10,000m2 になります。広いところに住んでいる人もいれば、狭いところに住んでいる人もいるのが満遍なく起こっている状況です。 グラフにするとこんな感じになります。
つまり、ミラフツ県には人口密度の高いところ中くらいのところ低いところが面積にして3分の1ずつあるということです。 このように、この集計が満遍ないとき、元の分布はロングテールになっています。ロングテール分布としてまず最初に取り上げられる「べき乗則」では、この集計は上記のグラフのように真っ平らになります。 (注:このことは逆に「べき乗則」はロングテール分布としては、現実にはあり得ない理論上の分布であることを示しています。なぜなら、これが必ず成り立つなら、100,000m2 のところも 0.1人住んでないといけないし、1m2 のところに 10,000人住んでいないといけないしと、両端に終わりがありません。現実は必ず両端は下がります。そのためにより現実のロングテール分布に近いものとして、たとえば DPLN分布といったものがあります。残念ながら、日本のウェブサイトにDPLN分布の情報はほとんどありません。たとえば The Double Pareto-Lognormal Distribution – A New Parametric Model for Size Distributions. といった論文を参照する必要があります。) さて、手元にある日本とアメリカのデータで、順位規模ごとの合計面積を集計すると次のようになります。
二国を比べるため正規化してしまっているので目盛りが小数点ばかりですが、左の方は広いところに住んでいる人の面積の合計、右の人は狭いところに住んでいる人の面積の合計になっています。 このグラフから分かることは、アメリカの方が一人あたり面積が多様であるということです。グラフ曲線が比較的平らだからです。人がまばらなところも、密なところもそこそこ同じくらいあるということです。 逆に日本は、人がまばらなところはあまりありません。日本の国土のほとんどは中くらいかそれより大きめの人口密度のところということになります。 言い換えると、アメリカの人は、住む場所として、人口密度が高いところから低いところまでより自由に選べますが、日本では人口密度が低い場所に住もうとしても、そういう場所は限られていることになります。順位規模ごとの合計値は簡単に計算できる
さて、順位規模ごとの合計値について集計しようとすると、結構手間です。エクセルなんかだと、規模ごとの区間を設定してそれに合うデータを合計して、とかなり時間がかかります。また、区間の区切りをあまり細かくするとデータがない箇所ができてなにかと面倒です。 しかし、素晴らしいことに、このグラフは簡単な計算で作ることができます。冒頭の方の一人あたり面積のグラフで、横軸を x、縦軸を f(x) とすると、新たに横軸はそのまま xで、縦軸を x・f(x) に置き換えるだけです。そうやって作ったのがこちら。
見事に同じ形になります(縦軸の数値が微妙に違うのは目をつむってください)。 この計算版は極めて強力です。この例ではデータの数が1700とか3100とかあるので同じ形がでますが、データの数が10個程度になると集計ではどうしようもありません。しかし、計算ならきちんと形が出るのです。順位規模ごとの合計値でロングテールを手なずけよう
このように、順位規模ごとの合計値のグラフを作ることで、ロングテールの全体的な傾向を把握することができるようになります。 なお、この順位規模ごとの合計値というグラフで解析する方法は他で見たことがありません。7年前くらいに考えて、ちょっと調べたり人に聞いたりしましたが、海外を含めてありませんでした。ましてや、 x・f(x)で、同じグラフが得られるというのも見たことありません。論文にしようかという話もあったのですが、専門分野でもなくて面倒なのでしてません。 ということで、この件はググっても他でもなかなか出てきませんが、7年間大変便利使っていますので、ロングテール扱う人には超お薦めです。ぜひこの方法を使ってロングテールを手なずけてください。 さて、このグラフについて何が起こっているか解説を加えておきます。前半にグラフに直線引いて立てたフラグの回収です。 -
市区町村別一人あたり面積をプロットしたらロングテールだった
2014-01-09 23:5932pt【ミラフツ名物ロングテール記事一覧 - NAVER まとめ】
未来の基盤である多様性はロングテール構造ができて初めて開花します。ロングテールを制するものは未来を制す。久々にロングテールネタです。 先日紹介した47mapsがおもしろいなーと思ってまた弄ろう思い、その準備に平成22年国勢調査(総務省統計局)都道府県・市区町村別主要統計表で、各市区町村の人口やら人口密度やらを弄り始めたのですが、そこでふと思いました。 普通人口密度で考えるけど、逆にしたら面白くね?
つまり、一人あたりの面積を考えるのです。(市区町村の面積)÷(市区町村の人口)。過疎に行くほど、大きくなる数字です。 もっとも広いところは、人口636人、面積390平方キロメートルの福島県檜枝岐村で、一人あたり61万平方メートル。 もっとも狭いところは、人口890万人、面積621平方キロメートルの東京都特別区部で、一人あたり70平方メートル。8700倍もの差があります。 で、これを広い方から順に全国民に並んでもらったとして、その面積をプロットしたのがこちら。
べらぼうに広いところに住んでいる人はごくわずかで、大部分の人はせま〜〜いところに住んでいるという、ロングテールっぽいグラフができあがります。 これだと本当にロングテールかどうかわからないので、両軸を1, 10, 100, 1000... という対数軸に取るとこうなります。
なだらかに右下に落ちていく、なかなかロングテールらしい曲線です。 できたのはまだここまでで、どれくらいロングテールなのかとか詳しくは解析できてないのですが、ロングテールであることは間違いなさそうです。 たとえば、ニコニコ動画の再生数というのもロングテールで、それは「わずかな再生数の動画が無数にある」からロングテールになります。アマゾンなら「わずかしか売れない商品が無数にある」です。 今回の例で言えば、「狭いところに住んでいる人が無数にいる」わけで、言われてみれば当然ロングテールになる事例と言えます。 きっと世界中様々な国で同じようなロングテールの分布が得られると思いますが、それらの分布を解析することで、より都市に集中しがちか、結構広がっているのかを評価できそうです。 このきっかけになった 「日本の人口分布って、どこまで偏ってるの?」の地図が簡単に作れた件 #blomaga では、日本では全人口の98%が国土の75%に広がっているのに対し、オーストラリアでは国土の25%に集中してるということになります。ちょうど反対という面白い結果になりました。
という結果が得られていますので、オーストラリアの方がより都市に集中しがちと言えそうですが、その度合いをロングテール分布の傾向を調べることでより詳細に把握できるわけです。 各国のデータ欲しいなぁ。 ちなみに、これに近い話題は以前取り上げたことがあります。 ロングテールの、ほとんど知られていない、しかしもっとも重要な性質(その2)~ロングじゃないテールの例~ そう、わざわざ「ロングテールじゃない」例として取り上げたもので、 -
[S馬]今週の馬車目線「山手線が止まった」
2014-01-08 23:1532pt【ミラフツ[S馬]今週の馬車目線 目次 - NAVER まとめ】
さて普段とは調子の違う記事を載せる水曜日。水曜日の馬車目線[S馬]として、現代社会頻繁に言われているけど、ちょっと立ち止まって考えてみたいパターンを紹介します。 前回紹介したパターンは「それは生産性というより、効率改善。」でした。
今回は「山手線が止まった」でした。 こんなツイートを拝見しました。
「やしきたかじんって誰?ローカルタレントの死亡ニュース流す必要あるの?」って思ってる東京の皆さん!!我々は「東京で雪が降った」だの「山手線が止まった」とかいう関東ローカルのニュースを今のあなたと同じ気持ちで見せられています!!
― たつなま (@tatsunama186) 2014, 1月 8
まあ首都圏以外に住んでいると毎日のようにこんな感じで、それは首都圏のローカルニュースだよなあというニュースが全国ニュースで取り上げられます。テレビのニュースだけではありません。yahooトップにも「山手線運転再開」とか出たりしますよね。 もちろん首都圏に住んでいる人は多いですから、それらを取り上げることで結果として視聴率とかアクセス数が取れるのでしょうし、つまりメディアとしては間違ってはいないのでしょう。 でもって、そういう状況について、別に目くじらたてて大騒ぎする人もほとんど見たことないですし、大半の人はふ〜んと生温く見ているのだと思います。 wikipediaの首都圏の人口を見ると、首都圏には全国の1/4くらいの人が住んでいますから、首都圏の話題はとても多くの人にとっての話題であることは間違いありません。でも、半分以上でもありません。いくら首都圏にたくさん住んでいるといっても、首都圏に住んでいる人と住んでいない人を比べると首都圏に住んでいる人の方が少数派です。 以前 普通は少数派 というエントリで取り上げたのですが、 -
「右脳バランス総集編」アップしました。
2014-01-07 16:4532pt昨年二ヶ月以上に渡ってお届けした「右脳バランス編」、まとめて読めるように一つにまとめてアップしました。 発想もめきめき20代からの右脳バランス 〜さそねっとブロマガ「未来の普通」右脳バランス総集編〜 このリンク先の記事を購入するとウェブで一気に読めるだけでなく、電子書籍のEPUB形式もダウンロードできます。お手元のデバイスでオフラインで読むことができます。EPUB形式をダウンロードするには、上記のリンク先の記事をニコニコポイントで購入して、タイトルの右の方にある「電子書籍」というメニューからダウンロードしてください。 このリンク先は昨年の日付でアップしたので、非会員の方も全33記事計1,065円分が半額以下の400円で購読できます。これまでの各記事の冒頭だけ読んで気になった方、ぜひご活用ください。 PDF版が欲しい、ニコニコポイント持ってないけど欲しいという方のために、こちらからも購入可能になっています。 以下は、総集編に加えたはじめにとおわりにです。それ以外は過去の記事をつなげてあります。 では、ハッピー右脳ライフお楽しみください。 はじめに これは、ブロマガ「未来の普通」2013年10月末から年末まで断続的に掲載された「右脳シリーズ」を集めた、題して「発想もめきめき20代からの右脳バランス」です。 このシリーズは感動的なプレゼンの宝庫TEDの中でも人気の一つ、 ジル・ボルト・テイラーのパワフルな洞察の発作 という動画に刺激されて始まりました。プレゼンターで脳科学者のジル・ボルト・テイラーさんは脳卒中で一時的に左脳が麻痺しましたが、そのご奇跡の復帰を遂げ、さらにはその間のことを克明に私たちに伝えることができたのです。 ジル・ボルト・テイラーさんは左脳に障害を持っている間言葉を失っていました。言葉でコミュニケーションしたり考えることができなくなっていたのです。それでもそれ以外の機能は維持していて、たとえば相手がどんな表情をしているのかといったことは問題なく理解できていたのです。 人間の脳は大きく分けて二種類の方法で情報を処理します。一つは左脳が得意な「逐次処理」で、ものごとを順番にこなしていく方法です。この方法は言葉で書き表すことができます。12×34という筆算をする時には、まず2×4をして、その答えと10×4の答えを足したものを線の下に書き、同じように12×3を計算したものを1けたずらして先の数字の下に書き、その両者を足しあわせると最後の答えが出るという感じです。言葉で説明できるので、学校などでの教育内容に向いていて、現在学習内容の大半は、この「逐次処理」で行うものが対象です。 また、順番に考えるので、過去ー現在ー未来のつながりを考えることができて、したがって「将来いい仕事につくために、今は遊ぶのを我慢して勉強をしよう」と計画を立てることができます。 一方、右脳は「並列処理」を得意とします。例えばこの絵で「赤い丸はどこにありますか?」と聞かれたら、
ヒトは一瞬で見つけることができます。丸の数が増えてもその速さはほとんど変わりません。ひとつひとつ丸を注視して赤か白かを見分けているわけではありません。左脳的な「逐次処理」ではない処理の仕方です。 あるいは会話をしているときに、相手がどんな感情なのかということも五感全てを使って、並列処理して感じ取っています。いちいち、「さっき言った言葉からはどう考えられるか」「次に表情はどうか」「体はどうか。揺すったりしてそわそわしてないか」「腕・手・指はどうなっていてそこからどう考えられるか」と順に考えたりしません。順に考えたら余計に間違えそうです。ものすごくそわそわしてもう会話を切り上げたそうなのが明らかな時に「まず言った言葉からどう考えられるか」なんて手順を踏む訳がありません。 しかし、この並列処理の方は、うまく言葉で過程を説明することができません。白い丸の中からどうやって赤い丸を見つけているのか説明しようと思っても「ここにあるものは、ここにある」としか言いようがありません。 もう一つ例を考えましょう。もし歯に何かものが挟まっていたら、「あー、歯にもの挟まってて気持ち悪い」と感じます。逆に特に大きなものが挟まっていないとき、挟まっていないことをどうやって感じているでしょう。別に左奥の上の歯の間から順番に右に向かって「挟まってないな」という感触を感じなくても、「うーん、今別に大丈夫」と一瞬で判断できます。これもどうして一瞬でわかるのか説明せよと言われていも、上手く説明できません。 こんな風に脳みそは、その過程を言葉にすることは難しいけれどうまく処理していることがたくさんあります。恐らく左脳的な逐次処理で考えることと同じくらいには、右脳的な並列処理でも考えています。 しかし、それは言葉にならないため、ほとんど意識されていなかったのではないでしょうか。ここのところは科学が大きく発達したこともあり、「言葉で説明できないものなどない」という価値観が受け入れられているように思います。しかし、このように実は頭の中は「言葉で説明できない処理」だらけだったのです。 念のため補足すると、赤丸を選ぶ仕組みも、脳科学的に言葉できちんと説明することはできているかもしれません。しかし、ポイントはそのように説明されていようといまいと、あるいはその仕組みがどんなものか知らなくても、私たちはその仕組みを利用できるし、しているということです。 このように、言葉ではうまく説明できないけれど、左脳と同じくらい膨大な処理を行っている右脳について、けれど、普段私たちはあまり意識していません。私自身もそうでした。 しかし2ヶ月以上前、ジル・ボルト・テイラーさんの動画を見て、右脳について考えたことを1日分の記事として書いたところ、後から後から右脳的な並列処理の世界が関わっているさまざまなことが気になり出し、1つ、2つと記事は増えていきました。 結果、二ヶ月とちょっとに渡って全部で33記事になりました。つまり、言葉を変えれば行き当たりばったりに書き綴られたものですが、大まかには以下のような構成になっています。 パート I /一時的に左脳を失った科学者の話が悩ましい 全てのきっかけになった記事です。一時的に左脳が麻痺していたジル・ボルト・テイラーさんの体験は神秘的でいわゆる「神を見た」という体験そっくりです。つまりこれらの体験の元は実は誰の中にでもあるけど、普段は言葉で考える左脳の影響が大きすぎて、特殊な状況でのみ見られるもののようです。神秘的体験の元である右脳が持つイメージについて考え始めた最初の記事です。 パート II /右脳バランス 次の二つの記事は、右脳的に生きるか左脳的に生きるかという二者択一な過ごし方ではなく、両者のバランスが取れた状態を考えて、そのようにバランスを取るにはどうすればいいか、またバランスを取ることが自分自身が豊かに暮らせることにつながる(雲を見上げるだけでも楽しくなる)だけでなく、ジル・ボルト・テイラーさんも提唱する世界がより平和になるのではないかという点について考えています。もともとここで終わるつもりだったのですが、あと30個も増えることになるとは。 バートIII /右脳を左脳で理解する試み 次は、8回に渡って、ときおり単独のコラムも交えながら、「右脳を左脳で理解する試み」という記事です。ジル・ボルト・テイラーさんの語る右脳の持つイメージが、自然界に生きる動物の価値観に似ているのではないかという点や、座禅など瞑想の極限で得られるイメージにも似ていることが分かったことから、右脳の持つイメージについて、左脳的な「言葉」でいろいろとその姿を捉えようとしています。子供は大人より右脳バランスが良く思えることについても考えています。また、右脳のイメージが特殊な状況でしか得られない理由も考えています。 パートIV /迫り来る「右脳革命」に20代が備える方法 そして最後のパートは、全14回に渡って、やはりときおりコラムも交えながら、迫り来る「右脳革命」に20代が備える方法という記事です。 今まで神秘的な体験として言わば得体のしれなかった右脳のイメージは、既にその存在はゆるぎないものになってきました。脳波も手軽に測定できるようになってきていて(実機での測定もでてきます)、今後は右脳や左脳が働く様子を客観的に測定できるようになるでしょう。 となると社会は今まで中心的だった左脳的な思考法だけでなく、右脳的な思考法も意識するようになります。左脳的思考能力の開発は現状飽和状態で、大学入試・就職面接なども技術的対策をこなした人程有利な状況ですから、今後当面は右脳的思考力を伸ばすことが社会の中でも大きな意味を持つことでしょう。 よく考えれば、言葉で考えているのは左脳だけです。脳には右脳だけでなく脳幹や海馬といったところもありますし、その他体全体(たとえば胃腸)なども言葉を持つ訳ではありません。しかし、それらすべて言葉がなくとも気まぐれではなく一貫した機能を持って、日々生きています。それらの機能を言葉で説明しなくても、問題なく生きていけます。そもそも動物はほとんど言葉を持ちません。つまりまず自分たちの体はその大部分が「言葉で説明できなくても動いている」のです。 世の中も同じです。自然も社会も「言葉での説明があろうがなかろうが」動いているものだらけです。もしかしたら、なんでもかんでも言葉で説明できるのかもしれませんが、説明など知らなくても利用したり関わっているものが大半です。「世の中説明してないものだらけ」なのです。 それらのものとつき合う、あるいは理解しようするのに、無理に言葉で理解しようとせず、言葉は持たないけれど並列処理である右脳的思考の方がうまくいくこともたくさんあるはずです。つまり、「右脳革命」の第一段階は、「世の中に言葉で説明できないものはないはず」などとつっぱらずに、「とりあえず世の中説明できてないものだらけ」ことを受け入れること、そして第二段階はそのうちの一部とは、無理に言葉で理解しようとしないで、右脳的思考で対応していこうという方向性を持つことです。 しかし、右脳的思考力を伸ばすのには発想の転換が必要です。 この厳しい競争社会を生き延びるために、右脳的思考力を伸ばそうと思うなら、それはすでに左脳的発想です。右脳は競争社会なんて好きじゃないし、「共創」社会を望んでいるし、つまり右脳的思考力が伸びたら、その分より多くの人が豊かに幸せになることを望んでいます。そんな右脳と仲良くなるには、今までの常識的な切り口はかえって邪魔になります。 では迫る「右脳革命」にどのように備えればいいのか、現時点で考えられる点についてこのパートでは記事にしました。特に、右脳的な思考を目指すことで、目下現実的に目に見えそうな成果は発想が豊かになることです。その発想法について詳しく考えています。 これらの記事を通して、今まであまり意識してこなかったけれど、自分の体や脳の中に、とても豊かな右脳の世界が広がっていることを感じられると思います。たとえば、空を見上げ雲を眺めているとき、言葉としては漠然と「きれいだなあ」しか浮かばなくても、それは脳みそがさぼっているわけではなくて、全身で空や雲を楽しんでいると分かります。人によっては、何を今さら、それが当たり前と思うかもしれません。まさに「考えるな、感じろ」という奴ですし。その世界は、自然を堪能するためだけでなく、発想力など様々なことに関わっているのです。 その世界があると確信さえできれば、その世界と慣れ親しんで行くのは時間の問題です。既に右脳的思考力は手に入れたも同然です。発想力もどんどん豊かになることでしょう。 それでは、連載を通して、右脳の世界に気付いてから、徐々にその様子が見えてくる過程をぜひお楽しみください。
2 / 3